- БЕСКОНЕЧНОСТЬ
[бесконечное]. 1. Одно из свойств Божиих; 2. Фундаментальная категория человеческого мышления; философское и богословское понятие, обозначающее безграничность и беспредельность как в бытийственном, так и в познавательном смысле. Вопрос о Б. возникает на всем протяжении истории культуры в самых разнообразных формах, напр. проблема Б. (или конечности) мирового пространства, времени, количества вещей в мире. Сюда же относится и вопрос о возможности бесконечного деления континуума, выделении в нем точек. Наконец, более изощренной логической техники требует обсуждение вопроса о существовании разных «типов» бесконечного. Вопросы о логической и онтологической природе Б., о ее статусе в Боге и в тварном мире получали разные решения и обоснования в философии, богословии и истории науки.
Потенциальная и актуальная Б.
Рус. слово «бесконечное» имеет значение отрицания: бес-конечное есть не конечное (аналогично и лат. infinitum). Это отрицание понимается двояко: или как частичное - то, что может превзойти любое конечное, или как полное - то, что актуально превосходит любое конечное. Уже в схоластике XIII-XIV вв. (Вильям Шервуд, Вильям Хейтесбери) это различие осознается и обозначается соответственно как «синкатегорематическая» и «категорематическая» Б. Из схоластики же (Григорий из Римини) идет и др. наименование этих подходов к бесконечному: «потенциальная» и «актуальная» Б.
Бесконечное в истории философии и богословии
Античная мысль в основном рассматривает бесконечное (греч. τὸ ἄπειρον) как неоформленное, как неставшее и, следов., несовершенное. В пифагорейском списке противоположностей бесконечное стоит на стороне дурного (злого). Бытие в античной мысли тесно связано с категорией меры и предела; бесконечное в этом отношении выступает как бес-предельное, без-граничное, почти не существующее (греч. μὴ ὄν). Бесконечное есть нечто близкое к хаосу, а иногда и отождествляется с ним. У Платона и Аристотеля бесконечное сближается с категорией материи как бесформенным и в силу этого как бы несуществующим под-лежащим субстратом вещей. Бытие вещи доставляется идеей (или формой), к-рая о-граничивает бесконечное, осуществляя «вписывание» вещи в упорядоченное единство космоса. Более позитивно использует категорию бесконечного Анаксимандр, главным началом его космологии является апейрон (греч. ἄπειρον букв.- без-граничное), из к-рого возникают и в к-рый возвращаются все вещи. У Левкиппа и Демокрита бесконечное пустое пространство содержит бесконечное количество атомов, образующих бесконечное количество миров. Однако господствующее отношение к Б. в античности все же иное. В окончательном виде оно было выражено Аристотелем. Для Аристотеля Б. существует только потенциально как возможность безграничного изменения (Phys. III 6. 207а 22-27). Не существует ни актуально бесконечного тела (конечен сам космос), ни бесконечной последовательности причин (в противном случае, по Аристотелю, отсутствовала бы первоначальная истинная причина движения). Актуально бесконечное не дано ни чувствам, ни уму. Потенциальная Б. реализуется у Аристотеля для чисел в направлении возрастания - натуральный ряд, а для величин в направлении убывания - потенциально бесконечное деление данного отрезка. Непосредственно зависящая от этого круга идей античная математика всегда мыслит свои «прямые» и «плоскости» как конечные, хотя и произвольно большие отрезки или куски плоскостей (в отличие от новоевроп. математики, в к-рой уже с XVII в. начинают рассматривать бесконечные прямые, напр. в проективной геометрии). В неоплатонизме постепенно, не без существенного влияния вост. мистики, пробивает себе дорогу новое положительное понимание бесконечного. Переходной ступенью служат здесь философские взгляды Филона Александрийского, давшего эллинистическую транскрипцию библейского понимания Божества.
Решительный перелом в отношении понятия бесконечного в европ. культуре происходит с утверждением христианства. С одной стороны, актуальная Б. является существенной характеристикой христ. Бога, бесконечно могущественного, бесконечно мудрого, бесконечно благого. Для христ. мысли, т. о., появляется бесконечный «предмет», к-рый можно познавать и о к-ром можно размышлять. С др. стороны, это «освоение бесконечного Бога мыслью» не может не иметь своих границ. Поэтому христ. богопознание разделяется на апофатический и катафатический методы.
Однако и само представление об актуальной Б. Бога в раннем христ. богословии имело альтернативу, напр. в учении Оригена, у к-рого явственна зависимость от греч. философской мысли. По Оригену, Бог не может быть бесконечным, т. к. бесконечное не имеет формы и немыслимо; высшее совершенство Бога и его конечность необходимо связаны (De princip. II 9. 1). Но уже блж. Августин задает вопрос: неужели Бог не может мыслить всех чисел (натуральный ряд) разом? Конечность Бога несовместима, по Августину, с Божественным достоинством (De civ. Dei. XII 18). Поскольку человек, как образ Божий, несет на себе «отпечаток» совершенств Творца, закономерным было появление представления о бесконечном и в тварном мире. У Альберта Великого и Фомы Аквинского еще полностью господствуют аристотелевские запреты: в мире не может существовать актуальная Б. Даже точки континуума существуют в нем только потенциально. Признание присутствия актуальной Б. в творении исторически было тесно связано с обсуждением природы человеческой души. Если душа человека несет в себе образ Божий, то в какой степени Божественные совершенства отразились в ней? Иоанн Дунс Скот настаивал, что человеческая душа по своей природе превосходит ту конечность, к-рая характерна для всего тварного: ведь душа способна воспринимать Божественную благодать. Значит, ей дарована нек-рая, адекватная «предмету» восприятия, бесконечная воспринимающая способность (Ordinatio. I. D 2. P. 1, q. 2, n. 130). Еще дальше идут мистики. Майстер Экхарт учит, что в глубине человеческой души имеется нетварная Божественная «искорка». Как соприродная Богу, эта «искорка», естественно, актуально бесконечна. Подобное понимание образа Божия прокладывало дорогу пантеизму и не раз осуждалось католич. Церковью. Кард. Николай Кузанский развивает свою концепцию о совпадении абсолютного максимума и абсолютного минимума. В этой концепции бесконечное, абсолютный максимум, становится «адекватной мерой» всех конечных вещей (Об ученом незнании. С. 109). Аналогично и в рамках пантеизма Б. Спинозы оказывается, что omnis determinatio est negatio (лат.- каждое определение есть отрицание): не через предел, не через ограничение бесформенной материи получают вещи свое бытие, а именно от подлежащей бесконечной Божественной субстанции, внутри к-рой самоопределение выступает как частичная негация (Этика. 1999. С. 253-273, 325).
Спекулятивная теология Николая Кузанского порождает представления и о Б. вселенной. Бог является «основанием» мира: то, что содержится в Боге «в свернутом виде», мир «разворачивает» в пространстве и времени. Пространственная протяженность мира и время его существования не могут быть конечными, потому что они «выражают» Б. Бога. Хотя мир не является бесконечным в том же смысле, как бесконечен Бог,- мир не есть все, что может быть,- тем не менее его привативная Б. (не infinitum, а indeterminatum) включает в себя Б. пространства и времени (Об ученом незнании. С. 99, 120). Пересмотр Н. Коперником геоцентрической системы и полемический талант Дж. Бруно помогают этому тезису Николая Кузанского стать популярным к XVIII в.
В целом в понимании бесконечного зап. богословской традиции не удается избежать ни аристотелевского финитизма, ни «энтузиазма» мистиков: бесконечное или всегда лишь только «по ту сторону» человеческого разума, или самонадеянно объявляется «достигнутым» пантеистическими мистиками.
Перспектива др. интерпретации бесконечного и его присутствия в творении раскрывается в правосл. учении о нетварных Божественных энергиях. Различая в Боге сущность и энергии, свт. Григорий Палама в сер. XIV в. утверждает правосл. учение о непостижимости Божественной сущности, но возможности познания бесконечного Бога в Его нетварных энергиях (Триады в защиту священно-безмолвствующих. М., 1995).
Среди философов Нового времени идею беспредельности мира поддерживал Р. Декарт: хотя и «недопустимо рассуждать о бесконечном, но следует просто считать беспредельными вещи, у которых мы не усматриваем никаких границ,- таковы протяженность мира, делимость частей материи, число звезд и т. д.» (Первоначала философии. С. 324). Кроме того, по Декарту, бесконечна человеческая воля, являющаяся существенным признаком образа Божия в человеческом существе. Именно несоответствие конечности человеческого разума и Б. воли служит, по Декарту, причиной ложных суждений (Там же. С. 327-328).
На фоне др. философов XVII в. наиболее убежденным защитником существования актуальной Б. выступает Г. В. Лейбниц. Тема Б. обсуждалась им в разных аспектах. Актуально бесконечно прежде всего количество субстанций-монад в универсуме. Каждая часть материи представляет собой также актуально бесконечную совокупность монад. Устойчивость агрегатов этих монад связана с особыми принципами их подчинения и с законом предустановленной гармонии. «Всякую часть материи можно представить наподобие сада, полного растений, и пруда, полного рыб. Но каждая ветвь растения, каждый член животного, каждая капля его соков есть опять такой же сад или такой же пруд» (Монадология. 67). В свою очередь, каждая монада представляет в своих восприятиях весь бесконечный универсум, бесконечный как в пространстве, так и во времени. Это понимание ведет Лейбница в психологии к формулировке концепции бесконечно малых («подсознательных») восприятий, в математике - к особому пониманию структуры пространственного континуума и, наконец, к созданию дифференциального и интегрального исчислений. Лейбницевские идеи в отношении актуальной Б. остаются в высшей степени действенными и по существу непревзойденными все последующие 3 столетия.
Взгляды И. Канта в отношении Б. двойственны, они отражают двойственность его философии в целом. В «Критике чистого разума» с т. зр. его философии математики невозможны ни бесконечное число, ни бесконечная величина. Мир в отношении своих пространственных и временных характеристик выступает ни как конечный, ни как бесконечный, а как indefinitum - неопределенный (Критика чистого разума. С. 389-501). В кантовской философии морали актуальная Б. находит определенное место, по-своему отражая общую традицию европ. христ. философии, видящей в человеческой душе образ Божий (Критика практического разума. С. 441-484). Практический разум при стремлении к высшему благу приходит к необходимости постулирования бессмертия души, существования Бога и свободы, оказывающихся актуально бесконечными. У И. Г. Фихте, по-своему разрабатывавшего идею Экхарта о причастности человеческого духа Божественной сущности, вся природа выступает уже как бледное отражение истинной Б., заключенной в абсолютном «Я». У Г. В. Ф. Гегеля конечное и бесконечное являются лишь 2 терминами в его диалектической триаде. Простое отрицание конечного дает «дурную Б.»: никогда не завершающийся переход от одного конечного к др. представляет собой только «долженствование бесконечного». Истинная Б. должна диалектически снять оба момента. Истинно бесконечен у Гегеля, собственно, Абсолютный дух, к-рый одновременно и актуально бесконечен и осуществляет свое развитие через мир конечных духов (Наука логики. С. 111-137).
В кн. «Парадоксы бесконечного» (1851) чеш. математик и философ Б. Больцано сделал попытку опровергнуть традиц. возражения против актуально бесконечного; он также рассматривает понятия, ставшие в дальнейшем главными и для нем. математика, создателя теории множеств Г. Кантора: различение потенциальной и актуальной Б., трансфинитного и абсолютного и ряд др.
С XX в. философские дискуссии вокруг проблем бесконечного соотносятся обычно тем или иным образом с теорией множеств и проблемой оснований математики. Таковы, напр., феноменологический подход к проблемам теории множеств у О. Беккера (Becker O. Mathematische Existenz. Halle, 1927); интерпретация проблем теории множеств как выражения классического конфликта между аристотелевским концептуализмом и платонистской традицией в математике у Л. Брюнсвика (Brunschvicg L. Les étapes de la philosophie mathématique. P., 1922); рассмотрение канторовской иерархии бесконечного на фоне концепции всеединства у Б. П. Вышеславцева (Этика преображенного эроса. М., 1994).
Бесконечное в математике и логике
Понятие актуально бесконечного эффективно применяется в математике, начиная с изобретения дифференциального и интегрального исчислений в XVII в. Однако убедительного обоснования этого использования бесконечного не удавалось найти более 2 веков. Особая фаза исследований начинается с сер. XIX в. Большую роль сыграли труды К. Вейерштрасса, Р. Дедекинда и в особенности Кантора. Они систематизировали употребление понятия бесконечного в европ. математической традиции, выделили его основные аспекты и предложили (Кантор) беспрецедентную конструкцию «шкалы бесконечностей», ведущую от самых простых типов бесконечного до «бесконечного в Боге». Кантор построил определенный аналог для понятия количества в случае бесконечных множеств (кардинальные числа). Одновременно им была развита и теория трансфинитных ординальных чисел: обобщение понятия порядкового числа в бесконечные совокупности. Построенная арифметика кардиналов (и ординалов) обладала довольно парадоксальными свойствами (напр.: 2 \bullet =

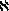 , где - кардинал, соответствующий множеству натуральных чисел), нек-рые из них, впрочем, были символическим выражением давно известных парадоксальных свойств актуально бесконечных множеств (напр., того, что четных и нечетных чисел во множестве всех натуральных «одинаковое количество»).
, где - кардинал, соответствующий множеству натуральных чисел), нек-рые из них, впрочем, были символическим выражением давно известных парадоксальных свойств актуально бесконечных множеств (напр., того, что четных и нечетных чисел во множестве всех натуральных «одинаковое количество»).
Однако в теории множеств уже с 90-х гг. XIX в. возникли и принципиально новые апории, к-рые не были разрешены в течение XX в. Одна из них, «парадокс Бурали-Форти», показывает, что, хотя и можно определить сколь угодно большой ординал b, однако рассмотреть всю шкалу ординалов Ω как единое множество невозможно: оно оказывается противоречивым. Тем самым одна из главных интенций Кантора - иметь возможность рассмотреть любой потенциальный процесс как законченный - потерпела крушение. Как пишет чеш. математик XX в. П. Вопенка, «теория множеств, усилия которой были направлены на актуализацию потенциальной бесконечности, оказалась неспособной потенциальность устранить, а только смогла переместить ее в более высокую сферу» (Математика в альтернативной теории множеств // Новое в зарубежной науке. Математика. М., 1983. № 31. С. 124). «Парадокс Рассела» указывает на противоречивость понятия множества всех множеств, не являющихся элементами самого себя. Это привело к выделению предикативных и непредикативных свойств множеств и построению т. н. теории типов, к-рую Б. Рассел развивал совместно с А. Н. Уайтхедом. Парадоксы теории множеств сказывались и на «макроуровне»: напр., в «парадоксе Банаха-Тарского» утверждается, что, используя систему аксиом теории множеств Цермело-Френкеля, можно разбить шар на конечное число частей, к-рые можно переставить так, что получится два шара, такого же размера, что и исходный.
Теория множеств оказалась естественным языком для решения стоявшей веками задачи арифметизации континуума. Во 2-й пол. XIX в. было предложено неск. арифметических конструкций действительных чисел (Вейерштрасс, Дедекинд, Кантор). Мощность получающихся числовых моделей континуума оказывалась равна 2
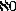 . Кантор предположил, что 2
. Кантор предположил, что 2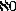 = , где - наименьшая из мощностей, больших - мощности множества натуральных чисел: {1,2,3,...\\. Это утверждение называется «континуум-гипотезой». Но, несмотря на пламенную веру Кантора в истинность результата, ни ему, ни последующим математикам не удалось доказать этот факт. Более того, из совместных результатов К. Гёделя (1939) и П. Дж. Коэна (1963) следует независимость континуум-гипотезы от остальных аксиом системы Цермело-Френкеля. Др. словами, континуум-гипотеза не может быть ни доказана, ни опровергнута в теории, опирающейся на эту систему аксиом. Философский смысл полученных результатов в том, что если мощность континуума равна какому-то «алефу» (необязательно ; т. е. обобщенная континуум-гипотеза), то континуум как бы «конструируется из точек». Однако доказать это в рамках известных аксиоматик теории множеств оказалось невозможным.
= , где - наименьшая из мощностей, больших - мощности множества натуральных чисел: {1,2,3,...\\. Это утверждение называется «континуум-гипотезой». Но, несмотря на пламенную веру Кантора в истинность результата, ни ему, ни последующим математикам не удалось доказать этот факт. Более того, из совместных результатов К. Гёделя (1939) и П. Дж. Коэна (1963) следует независимость континуум-гипотезы от остальных аксиом системы Цермело-Френкеля. Др. словами, континуум-гипотеза не может быть ни доказана, ни опровергнута в теории, опирающейся на эту систему аксиом. Философский смысл полученных результатов в том, что если мощность континуума равна какому-то «алефу» (необязательно ; т. е. обобщенная континуум-гипотеза), то континуум как бы «конструируется из точек». Однако доказать это в рамках известных аксиоматик теории множеств оказалось невозможным.
Концепция бесконечного, являясь своеобразным символом Божества в сфере науки и философии, в своих конкретных экспликациях неизбежно касается религ. сферы, как в богословском, так и в экзистенциально-духовном плане. Характерно, что разработка концепции бесконечного наложила отпечаток на факты личной биографии ее создателей. Кантор, напр., пытался дать «богословские применения» своим конструкциям с актуальной Б., твердо веря в то, что построение и утверждение в науке теории множеств было миссией, возложенной на него Самим Богом. Кантор различал 3 типа бесконечного: бесконечное в Боге («в уме Бога») - Абсолютное, в тварном мире - трансфинитное, в уме человека - трансфинитные числа (ординалы). Несмотря на то что в канторовской философии математики критерием научности служила лишь логическая непротиворечивость, для оправдания теории множеств он в высшей степени нуждался в доказательствах существования трансфинитного (бесконечного) в мире. Это послужило бы не только опровержению аристотелевской концепции, но и явилось бы опорой для программы развертывания новых подходов в физике и химии на основе теории множеств. Кантор пытался толковать известное место из Книги Премудрости Соломона (11. 21): «...Ты все расположил мерою, числом и весом» - как подтверждение существования трансфинитного в мире. «Здесь не стоит,- писал он,- in numero finito (конечным числом.- В. К.)» (Meschkowski H. Aus den Briefbüchern Georg Cantors // Archive for History of Exact Sciences. B.; Hdlb.; N. Y., 1965. Vol. 2. N 6. S. 512), и поэтому, по Кантору, не следует этот текст использовать в качестве аргумента против бесконечных чисел. Существование трансфинитного в мире, как более подобающего бесконечному и всемогущему его Творцу, Кантор пытался доказать и в переписке с католич. богословами. Это вызвало справедливую критику последних, обвинивших Кантора в склонности к пантеизму.
В общефилософском плане теория множеств выступает как факт характерного самоопределения науки кон. XIX-XX в., доводящий до логического предела основные научно-философские интенции, заложенные еще в XVII в.: редукционизм, конструктивизм, формализм. В этом смысле дискуссии вокруг оснований теории множеств естественно перекликаются с др. известными феноменами культуры модерна: формализмом в искусстве, социализмом, фрейдизмом, евгеникой, генной инженерией. Трагические коллизии мысли, связанные с историей т. н. парадоксов теории множеств, представляют собой отчасти своеобразное раскрытие и саморазоблачение тех титанических человекобожеских импульсов, к-рые сыграли существенную роль в становлении новоевроп. науки и цивилизации в целом в XV-XVII вв.
Лит.: Больцано Б. Парадоксы бесконечного. Од., 1911; Бруно Дж. О бесконечности, вселенной и мирах // Диалоги. М., 1949. Самара, 2000п. С. 323-480; Спиноза Б. Этика // Избр. произв.: В 2 т. М., 1957. Т. 1. С. 359-618. СПб., 1999п. Т. 1. С. 251-478; Becker O. Grösse und Grenze der mathematischen Denkweise. Freiburg; Münch., 1959; Кант И. Критика чистого разума // Соч.: В 6 т. М., 1964. Т. 3; он же. Критика практического разума // Там же. Т. 4 (1); Heimsoeth H. Die sechs grossen Themen der abendländischen Metaphysik und der Ausgang des Mittelalters. Stuttg.; B., 19655; Френкель А., Бар-Хиллел И. Основания теории множеств. М., 1966; Коэн П. Дж. Теория множеств и континуум-гипотеза. М., 1969; Беркли Дж. Аналитик, или Рассуждение, адресованное неверующему математику // Соч. М., 1978. С. 395-442; Dauben J. W. Georg Cantor: His Mathematics and Philosophy of the Infinite. Camb.; L., 1979; Николай Кузанский. Об ученом незнании // Соч.: В 2 т. М., 1979-1980. Т. 1. С. 47-184; Лейбниц Г. В. Монадология // Соч.: В 4 т. М., 1982. Т. 1. С. 413-429; Гегель Г. В. Ф. Наука логики. СПб., 1997; Кантор Г. Труды по теории множеств. М., 1985; Декарт Р. Первоначала философии // Соч.: В 2 т. М., 1989. Т. 1. С. 297-422; Флоренский П., свящ. О символах бесконечности // Соч.: В 4 т. М., 1994. Т. 1. С. 79-128; Катасонов В. Н. Боровшийся с бесконечным: Филос.-религ. аспекты генезиса теории множеств Г. Кантора. М., 1999.
В. Н. Катасонов
Православная энциклопедия. - М.: Церковно-научный центр «Православная Энциклопедия». 2014.
